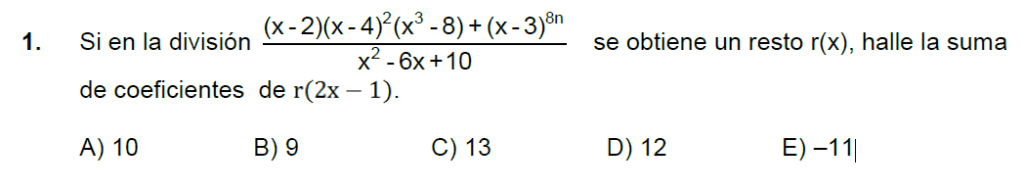ÁLGEBRA Semana N° 19
Contenidos:
ToggleRepaso
Álgebra S19 P 1/5
En esta clase se desarrollan dos ejercicios propuestos en la semana 19 del curso de álgebra.
El primer ejercicio plantea una división de polinomios en la que se debe hallar el resto r. Para resolverlo, se aplica el teorema del resto, igualando el divisor a cero, despejando la variable y reemplazando en el dividendo para obtener r. Luego se evalúa r en un punto dado y se calcula la suma de sus coeficientes.
El segundo ejercicio presenta un polinomio px completo y ordenado con una condición adicional. Se analizan dos escenarios, px ordenado de forma creciente o decreciente. Comparando con la condición dada, se descarta que sea creciente. Luego, conociendo el exponente menor, se calculan los demás coeficientes y se reconstruye px. Finalmente, se evalúa en 1 para obtener la suma de coeficientes pedida.
En ambos ejercicios se ponen en práctica conceptos estudiados durante el curso como división de polinomios, teorema del resto, tipos de polinomios y evaluación. Se explican paso a paso los procedimientos aplicados, recalcando los fundamentos teóricos utilizados.
Video Álgebra S19 P 1/5
Álgebra S19 P 2/5
En el primer ejercicio se presentan dos ecuaciones cuadráticas, una con soluciones complejas y otra con soluciones reales. Se pide determinar el valor entero de m para que se cumplan esas condiciones.
Para resolverlo, primero se analiza la primera ecuación y se determina que, para tener soluciones complejas, el discriminante debe ser menor que cero. Luego se resuelve la desigualdad correspondiente y se obtiene que m debe ser mayor que 5/4.
Después se analiza la segunda ecuación y se determina que, para tener soluciones reales, el discriminante debe ser mayor o igual a cero. Al resolver la desigualdad se obtiene que m debe ser menor o igual a 25/12.
Finalmente, se concluye que el único valor entero de m que cumple ambas condiciones es 2.
En el segundo ejercicio, se presenta una función cuadrática que modela la utilidad de la venta de casacas en función de la cantidad vendida.
Se pide calcular la suma de la máxima utilidad y la diferencia entre la máxima y mínima cantidad de casacas a vender para tener ganancias.
Para resolverlo, primero se calcula la máxima utilidad completando cuadrados, obteniéndose 625. Luego se halla la diferencia entre la máxima y mínima cantidad de casacas resolviendo la desigualdad de la utilidad mayor que cero. Se obtiene que la diferencia es 48.
Finalmente, se suma la utilidad máxima de 625 con la diferencia de 48, dando como resultado 673.
Video Álgebra S19 P 2/5
Álgebra S19 P 3/5
Se presenta un ejercicio donde se debe hallar el mínimo común múltiplo (mcm) de dos polinomios cúbicos p y q. Para hallar el mcm primero se debe factorizar los polinomios, para lo cual se utiliza el método de divisores dinámicos.
Luego de factorizar p y q, se construye el mcm tomando todos los factores primos comunes y no comunes. Los factores primos comunes se elevan al mayor exponente y se incluyen también los factores primos no comunes.
Posteriormente se evalúa el mcm resultante en el valor dado, que en este caso es -2.
En el segundo ejercicio, se presenta una expresión con dos polinomios elevados a la potencia 100. Se identifica que esta expresión representa un binomio elevado a la 100, por lo que su desarrollo tendrá 101 términos.
Se pide hallar el término central de este desarrollo, para lo cual se utiliza la fórmula del término central de un binomio. Luego, por analogía con la fórmula, se deducen los valores de m, n, p y q.
Finalmente, con estos valores se halla la expresión pedida en el enunciado, que corresponde a n+n-p-q.
En resumen, en estos ejercicios se pone en práctica la factorización de polinomios para hallar el mcm y se utilizan las fórmulas para el desarrollo de binomios con exponente entero para hallar el término central. Se logra identificar la estructura de las expresiones dadas para resolver los problemas planteados.
Video Álgebra S19 P 3/5
Álgebra S19 P 4/5
En el primer problema se plantea una ecuación con polinomios para determinar cuántas rosas le quedan a Pablo para obsequiar después de repartir unas entre sus amigas y considerando que dos rosas se marchitaron. Se explica el concepto del algoritmo de la división polinómica, donde se obtiene un cociente y un resto. Se recuerda que el grado máximo del resto es uno menos que el grado del divisor. Mediante sustitución de valores y resolución de ecuaciones, se halla el resto de la división. Considerando las dos rosas marchitas, se concluye el número de rosas que le quedan a Pablo para obsequiar. El propósito es recordar el algoritmo de la división polinómica.
En el segundo problema se plantea una situación con dos personas, Aarón y su hijo Lucio, cuya suma de edades actuales es 56 años. Luego de 18 años, la edad de Lucio será 5 años más que la mitad de la edad de Aarón. Se definieron variables para las edades actuales y se plantearon ecuaciones utilizando los datos. Resolviendo el sistema de ecuaciones se hallaron los valores de las edades actuales. La relación entre las edades es la respuesta pedida en el problema.
Video Álgebra S19 P 4/5
Álgebra S19 P 5/5
Optimización de Costos para Paseo de Trabajadores
Se plantea un problema de optimización donde una compañía debe enviar a 1200 trabajadores de paseo contratando buses de dos capacidades: 50 y 30 pasajeros. Se definen las variables x como la cantidad de buses de 50 pasajeros e y como la cantidad de buses de 30. Se establece que el costo de cada bus grande es 240 y el de cada bus pequeño es 110.
El objetivo es minimizar la función de costo, que es 240x + 110y. Se tienen dos restricciones: la empresa solo dispone de 28 conductores, por lo que x + y ≤ 28. Además, la cantidad total de asientos en los buses (50x + 30y) debe ser mayor o igual a 1200 para que quepan todos los trabajadores.
Se grafica el sistema de desigualdades, obteniendo una región poligonal. Según la teoría, los puntos extremos de la función objetivo estarán en los vértices de esa región. Calculando el costo en cada vértice, se obtiene que es mínimo cuando x=18 e y=10, con un costo de 5420.
Por lo tanto, para minimizar el costo la empresa debe alquilar 18 buses de 50 pasajeros y 10 de 30 pasajeros. De esta manera se resuelve el problema de optimización: encontrar la cantidad de cada tipo de bus que minimiza el costo total, sujeto a las restricciones dadas. Se han abordado los conceptos claves de optimización matemática: función objetivo, variables, restricciones y región factible.
Video Álgebra S19 P 5/5
Ejercicios de Álgebra Semana 19
Álgebra S19 2017 II
Se resuelven ejercicios de álgebra abarcando diversos temas como:
- Expresiones algebraicas: Se determina el coeficiente principal y grado absoluto de un monomio.
- Ecuaciones exponenciales: Se resuelve una ecuación con la variable en el exponente para hallar el porcentaje máximo de hierro en una aleación.
- Máximo común divisor: Utilizando el algoritmo de Ruffini, se halla el máximo común divisor de dos expresiones y se calcula la suma de sus cifras.
- Sistemas de ecuaciones lineales: Se resuelve un sistema de dos ecuaciones con dos incógnitas mediante determinantes para encontrar datos de un problema de palabras.
- Desigualdades e intervalos: Se halla el conjunto solución de una desigualdad con valor absoluto y se determina la menor y mayor solución entera.
- Producto de raíces de un polinomio: Dado el conjunto solución de una desigualdad, se forma el polinomio de menor grado con esas raíces.
- Binomios y técnicas de factorización: Se identifica el valor de n en un término de un desarrollo binomial.
- Logaritmos y ecuaciones logarítmicas: Se resuelve una ecuación logarítmica planteando primero la base y aplicando propiedades.
- Números complejos: Se halla la parte real de un número complejo dado su conjugado.
- Ecuaciones diofánticas: Se resuelve una ecuación diofántica mediante factorización y divisores mínticos.